贝特朗奇论

在单位圆内随机地取一条弦，其长超过该圆内接等边三角形的边长√3的概率等于多少？

这个问题看似简单，结果却让人大跌眼镜。我们可以用三个完全正确的方法，得到三个完全不同的答案！

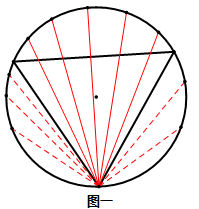
1.将弦的一段固定在等边三角形的某一个顶点上，然后另一端绕着圆周旋转。可以在图一中发现，只有当另一端点位于上方的圆弧时，这条弦的长度才会超过三角形的边长，由此可得所求概率为1/3。

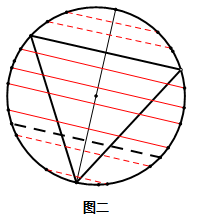
2.根据几何学原理，圆内弦的长度与弦到圆心的距离有关。从图二可以看出，当弦心距小于1/2时，这条弦的长度大于三角形边长，所以这样求出的概率为1/2。

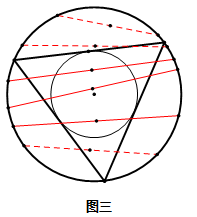
3.再来考虑一条弦的中点，根据图三可以得出：只有当弦的中点位于半径为1/2的小圆内部时这条弦的长度才满足要求，同时因为这个小圆的面积是大圆的1/4，所以所求概率也是1/4。

你能说出到底哪种方法是错的吗？如果它们都是对的，那么这样的一道客观题又怎么会有三个不同的答案呢？

其实这三种说法都是正确的。但是它们的结果之所以不同，只是因为它们各自对问题的理解不同，采用了不同的等可能性假定。在第一种方法中，我们默认的假设是“圆内弦的端点在圆周上是均匀分布的”；在第二种方法中，我们默认的是“圆内弦到圆心的距离是均匀分布的”；第三种方法默认的假设则是“圆内弦的中点在整个圆的内部是均匀分布的”。这三种假设对应着三种不同的求解方法。

需要说的是，随意指责哪个假设是不合理的有所不妥，因为它们都是有依据的。不妥的地方在问题本身，这个问题问的并不严谨，没有对问题中的“基本空间”进行定义，导致在解题人求解时只能够依靠自己的理解补充解题所需条件。如此一来，一问三解就不足为怪了。

上述问题被称为“贝特朗奇论”，是数学家贝特朗在上世纪初提出来的，用于批判当时尚不严谨的概率论。也正是在贝特朗工作的推动下，此后概率论的研究开始向公理化方向发展。

本福特法则

据说，1881年天文学家西蒙•纽康伯发现对数表以1起首的数所在的那几页较其他页破烂，由此他怀疑以1开头的数字就是比其他数多，大量统计之后发现果真如此。这个故事的真实性已无从考究，不过它可能是本福特法则第一次被注意到。

所谓本福特法则，是指在一堆从实际生活得出的数据中，以1为首位数字的数的出现概率约为总数的三成，是人们通常期望值1/9的3倍，它的确切值等于lg2，而越大的数字，以它为首位的数出现的机率就越低。更一般地，我们能够说明在r进制中，以n开头的数字出现的概率是 log _r (n+1)- log _r (n)。根据这个公式，可以制作出十进制下数字1~9开头的概率表：

开头	1	2	3	4	5	6	7	8	9
概率	30.1%	17.6%	12.5%	9.7%	7.9%	6.7%	5.8%	5.1%	4.6%

这个神奇的法则几乎完全违背了人们的直觉：哪个数字开头的概率不应该是一样的嘛！

维基百科上对此有个简单的解释：就数数而言，从1开始，历经1,2,3,...,9，到这点终结的话，以哪个数起首的几率是相同的，但9之后是10至19，到这里以1起首的数出现的几率又大大高于了其他的数。而在下一堆9起首的数出现之前，必然会经过一堆以2,3,4,...,8起首的数。如果这种数法一旦有个终结点，以1起首的数的出现率一般都会比9大。

也就是说，我们平时认为的“以1开头和以9开头的数字一样多”这种情况，实际只有在[1,999]此类区间里才会出现。任意给一个区间，由于样本的不完整性，基本不可能出现这种情况。从这里也可以看出，要想使得本福特法则生效，便不能对数字的区间范围进行明确的规定。

说到这里，大家自然会进而关心本福特法则在实际生活中的应用。我们可以在 这个页面 下方列出的表格中看到，不论是各国人口数量还是门牌号码都基本服从本福特法则，而且这些统计得到的结果和理论预测值的误差也很小。从而这些生活中的实例也说明了以1开头的数字确实是最多的，死理性派对此曾有过 详细的介绍 。

这个法则最经典和广泛的应用是验证统计数据真伪。如果一个包含了几千个数字的样本居然完全不服从本福特法则，那么你可要小心了，这个样本很有可能是伪造的。而除此之外，本福特法则在会计、股票甚至是选举领域也有着重要的应用。

友谊悖论

你是广交朋友的闪亮交际明星还是人际贫瘠的宅男？也许这个问题刺痛了许多不善交际的技术男的心：总能看到某个朋友每天应酬繁多、应接不暇，而自己的手机却常年不响一声。

实际上几乎每个人都会觉得朋友的朋友总是比自己的多。换句话说就是自己的朋友数，几乎总是小于自己所有朋友的朋友数的平均值。

这个结论看上去很违背直觉：如果我是某个人的朋友，那个人必然也会是我的朋友，友谊是双向的，所以我们会经验的认为整个数据是平均分布的，任何人的朋友数和他的朋友比起来应当差不多。怎么可能他们的平均朋友数会比我们自己的多呢？然而这却是事实，或者唯一的安慰是一切与你无关，这不过是一个不寻常的统计学案例。

我们不妨看看下面的这个例子。

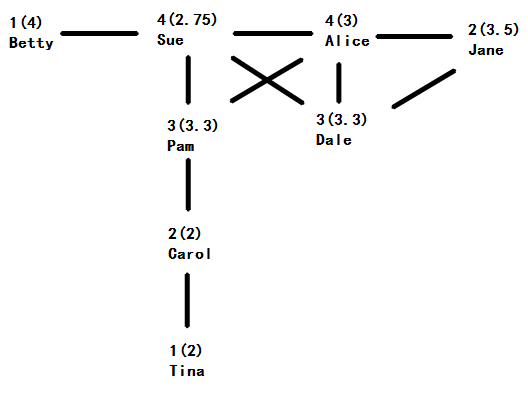
上图是八个女孩之间的朋友关系图，其中标注了每个人的名字、朋友数和她的朋友的平均朋友数（括号内的数字）。可以发现，只有Sue和Alice两个人的朋友数比她们朋友的平均朋友数要多。如果对所有括号里的数求均数，得到的结果约为2.98；但是这八个人的平均朋友数是2.5（10条关系线×2，除以人数8）。群体中所有人朋友的朋友平均数大于群体所有人的朋友平均数，这是为什么呢？

其实这个看起来有些不可思议的结论可以这样解释：有一百个人，他们都能有一个拥有一百个朋友的朋友，但是只有一个人，能有一个只有一个朋友的朋友。这句话算不上严谨，而且很绕口，但是实际上它传达了这样的意思：在计算“朋友的朋友”这个过程中，一个人拥有越多朋友则越容易被重复计算进来。比如在上图中，Sue有四个朋友，那么“Sue拥有四个朋友”这个条件在Sue的四个朋友分别计算自己的“朋友的朋友数”时，就被重复使用了四次。

让我们来做一个简单的数学推理：设群体总人数为n，第i个人的朋友数为Fi，那么群体所有人的朋友均数就是( ∑ Fi )/n。至于所有人“朋友的朋友”则一共有 ∑ Fi 个样本（把每个人的朋友列举一遍），又因为第i个人的朋友数会被重复计算Fi次，所以群体中所有人“朋友的朋友”的总数为 ∑ Fi ² 。于是其朋友的平均朋友数就是(∑ Fi ² )/( ∑ Fi )。根据均值不等式的变形可知，( ∑ Fi ² )/( ∑ Fi )≥( ∑ Fi )/n。如此一来我们就证明了在朋友圈里，朋友的平均朋友数不小于每个人的朋友均数。更精确地描述就是：

朋友的朋友均数=朋友均数+朋友数方差/朋友均数

当然，大家即便知道了这个事实也请不要灰心，你的朋友看起来总是拥有比你更多的朋友，其实只是某几个人际交往明星从中作梗，让你产生了这种错觉而已。

在数学中没有任何一个其他分支有这么多例子能说明直觉与经验会得出如此错误的结论，而正确的解答又与直觉矛盾。当人们看到一个概率或者统计的悖论时，第一反应是不相信，而在了解了真相后，紧接着的反应几乎必然是想清除疑云迷雾。所以，好好学学概率和统计这门课吧。

参考资料：

http://mathworld.wolfram.com/BenfordsLaw.html

http://www.jstor.org/stable/2781907